\begin{align*}
\begin{array}{c|c}
\text{Level} & \text{Damage Dice} \\ \hline
\text{1--3} & 1d6 \\
\text{4--7} & 1d8 \\
\text{8--11} & 1d10 \\
\text{12--15} & 2d6 \\
\text{16--19} & 2d8 \\
\text{20} & 2d10
\end{array}
\end{align*}
Table 1: Monk Damage Progression in D&D 3.5
For levels 1–11 things are pretty clear. Each time the damage dice increase it's strictly better. However, that's not true when moving from 1d10 to 2d6. Certainly, the minimum and maximum are both higher for 2d6 (2 and 12, respectively, as opposed to 1 and 10 for 1d10). The average is also better: 7 versus 5.5. But often we don't care about such metrics. For example, say our Monk is fighting some opponents that each have 5 hit points each. In such as case, we'd like to take them out in one hit as often as possible. Thus, the probability of rolling 5 or higher is of particular interest.
To consider the general case, let's look at the probabilities of rolling a given number or higher for each of the two damage rolls, as shown in Table 2.
\begin{align*}
\begin{array}{ccc}
x & P(1d10 \geq x) & P(2d6 \geq x) \\ \hline
1 & 1 & 1 \\
2 & 0.9 & 1 \\
3 & 0.8 & 0.972 \\
4 & 0.7 & 0.917 \\
5 & 0.6 & 0.833 \\
6 & 0.5 & 0.722 \\
7 & 0.4 & 0.583 \\
8 & 0.3 & 0.417 \\
9 & 0.2 & 0.278 \\
10 & 0.1 & 0.167 \\
11 & 0 & 0.0833 \\
12 & 0 & 0.0278
\end{array}
\end{align*}
Table 2: Monk Damage Probabilities at Levels 11 & 12
This is actually strictly better. But it makes you wonder whether there are cases where it looks like something is better, but it's actually worse. If we had looked at the pmf for 1d10 vs 2d6 we might have been misled, because at 10, 2d6 looks worse (lower probability of getting a 10), even though it is strictly better when considering the probability of rolling 10 or higher.
So let's change the question to be about the best weapon. There are many different weapons in Dungeons and Dragons. Even just looking at the 5th edition Player Basic Rules download, there is almost a full page table on page 47. Weapons differ in cost, dice rolled for damage, type of damage dealt, weight, and properties such as whether it is thrown, requires two-hands to use, etc..
To contain the discussion, let's first just focus on which does the most damage. A lot of the other characteristics of the weapon matter in very context-specific ways. Glancing through the table it's pretty easy to narrow down the list into two potential groups. Those weapons which do 1d12 damage (e.g. a greataxe), and those which do 2d6 damage (i.e. a maul). Both can do up to 12 damage. The maul always does at least 2 damage, so that's better. What about average damage? The average roll for a dN is $(N+1)/2$. This means the average greataxe damage is 6.5, while the average maul damage is 7.
Let's compare the distributions. We've already computed 2d6 for something else. 1d12 is pretty simple, $1/12$ for every possibility. Fig. 1 shows the probability mass functions (PMFs), while Fig. 2 shows the cumulative distribution functions (CDFs). We see some cases in which 2d6 is better, while in some cases 1d12 is better. Look at rolling at least a specific number, that's what matters, which is close to the complementary cumulative distribution function (CCDF), which is plotted in Fig. 3. Here we see that the probability of rolling towards the higher end of the damage distribution with a greataxe is greater than with a maul. Consider just the probability of rolling 12 or higher. With a greataxe the probability is $1/12$, with a maul it's $1/36$.
 |
| Figure 1: Damage PMF of Greataxe and Maul |
 |
| Figure 2: Damage CDF of Greataxe and Maul |
 |
| Figure 3: Damage CCDF of Greataxe and Maul |
Looking at just the probability of elimination in the first round is a small part of the analysis. Next, we'll look at the distribution of the the round in which the target is eliminated, $R$. To determine this, we need a straightforward way to check whether or not we've eliminated a target in a given round. In this case, I found it easier to look at the CDF of elimination, that is, the probability that the target is eliminated by a certain round of combat. In round $r$, we've rolled damage for each weapon $r$ times. If the damage if at least equal to the target's HP, then it must have been eliminated by round $r$. We previously learned how to use convolution to compute the PMF of rolling multiple dice. We can apply this iteratively to get the PMF of rolling $r$d12 for a greataxe or $2r$d6 for a maul in total by round $r$. Performing the running sum to get the CDF from the PMF is straightforward. Then the CDF of the round of elimination, $F_R(r)$, is given by,
\begin{align}
F_R(r) = 1 - F_{D(r)}(h-1) ,
\end{align}
where $D(r)$ is the total damage by the relevant weapon by round $r$ and $h$ is the number of hit-points of the target. Running through the computations for our selected targets we get the plots in Figures 4, 5, and 6. We can see that the maul is almost universally better. The two exception points are the aforementioned eliminating a hobgoblin in 1 round, as well as the probability of eliminating a bugbear in 3 rounds.
 |
| Figure 4: Probabilities of eliminating a goblin by a given round |
 |
| Figure 5: Probabilities of eliminating a hobgoblin by a given round |
 |
| Figure 6: Probabilities of eliminating a bugbearby a given round |
\begin{align}
\mathbb{E} R &= \sum_{r=0}^\infty P(R > r) \\
&= \sum_{r=0}^\infty 1 - F_R(r)
\end{align}
We can combine this with our earlier equation for $F_R(r)$ to come up with a simpler expressoin based on the CDF of the total damage up through round $r$.
\begin{align}
\mathbb{E} R &= \sum_{r=0}^\infty 1 - (1 - F_{D(r)}(h-1) ) \\
& = \sum_{r=0}^\infty F_{D(r)}(h-1) \\
\end{align}
While the above sum is shown over an infinite range, we know that it is limited. In the case of the greataxe, since we do at least 1 damage per round, we need only consider up to $h$ rounds. Similarly, for the maul, which does at least 2 damage per round, we need only consider up to $\lfloor \frac{h}{2} \rfloor$ rounds. The results are plotted in Fig. 7. While it's hard to see for low values of the target's HP, it clearly shows that the maul requires fewer rounds, on average, for any number of hit points.
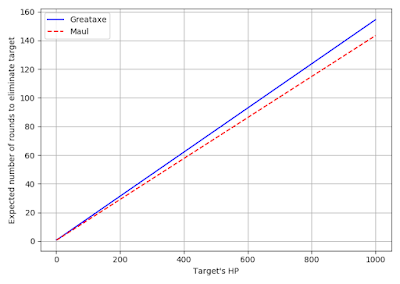 |
| Figure 7: Expected number of rounds to eliminate a target vs. hit points |
One might propose the following argument to approximate the number of rounds expected for elimination. Since we know the average damage per roll, all we must do is to take the target's HP and divide by this average damage to find the expected number of rounds to elimination. To aid in discussion of this thought, consider the plot in Fig. 8, which shows the expected number of rounds to elimination per target HP. Also plotted are asymptotes, which are equal to one divided by the average damage per round. That is, if this argument were true, the plot would coincide with these dotted lines. It is not true, and thus they do not coincide. However, they do seem to predict values which the curves are approaching asymptotically, as emphasized in Fig. 9. For a small number of hit points, the non-linear impacts of needing to roll a whole number of attacks means that the inverse of the average is a poor estimate. For example, to eliminate a target with only 1 HP, at 1 round is always needed. An attempt to incorporate this is shown in Fig. 10, which shows estimates of the $R$ per HP, by estimating $R$ as HP divided by the average damage per round, rounding up to the nearest integer number of rounds, and then dividing by HP. We can see that this shows a similar shape, but has discontinuities at various points, corresponding to when the number of rounds is rounded up to the next integer value. If we consider a target like the hobgoblin with 11 HP, there are a number of possible rounds of elimination. To determine $\mathbb{E}R$, first the distribution of $R$ is considered and then averaging is done. The plot in Fig. 10 averages first, and then tries to come up with the number of rounds. Since there is essentially non-linearity involved, we cannot change the order of the averaging without introducing error. The nonlinearity I'm talking about is this: in the round of elimination there may be some excess damage done. Going into that around you may only need to do 3 more points of damage, but it's likely that more damage will be done. Thus, this damage, while it contributes to the average damage per round, does not affect the number of rounds until elimination. As the number of hit points that a target has increases, this excess damage becomes less and less of an impact, which is why the plots approach the asymptotes. Across these plots we see that the maul is universally better than the greataxe.
 |
| Figure 8: Expected number of rounds per hit-point to eliminate a target vs. hit points |
 |
| Figure 9: Expected number of rounds per hit-point to eliminate a target vs. hit points (zoomed in) |
 |
| Figure 10: Expected number of rounds per hit-point to eliminate a target vs. hit points compared to a crude estimate\label |
That was a little disappointing. I was really expecting to find some scenarios where the greataxe is better. Sure, if we really need to eliminate a hobgoblin in 1 round it's better, but that's too specific to satisfy me. The consistency provided by rolling 2d6 just seems to overpower the slightly better chance of a high roll on 1d12. So what if we compare against something that we might expect to be worse. What if we compare 1d12 to 2d4? When we look at the same comparison, shown in Fig. 11, we see that for target HP less than 5, rolling 2d4 results in a faster expected elimination. Here, the higher minimum appears to prevail over the lower average damage, the latter of which wins for large target HP.
 |
| Figure 11: $\mathbb{E}R$ for 1d12 and 2d4 |

