Is it possible an event is never drawn?

A deck of cards with values in a 2d3 distribution (so a single card with a value of 2, two value 3 cards, etc) and a 10th reshuffle card. On a reshuffle card, draw a replacement card, until you get a value (ie not the reshuffle) card. I was going to add another card that has a specific in-game event, and was trying to work out how likely it was that card would appear before the game ends (about 50 draws, not tied to the cards): I think it is possible, albeit unlikely, that it may not appear to all (although the longer the game goes on, the less likely that is, from my understanding of probabilities).

—paraphrased from here on BGG

This can be solved with a Markov chain, which is a way to model sequences of probabilistic events, where the probabilities involved can be expressed in terms of the state after the previous step in the sequence. In this case, the state represents what's still in the deck. We'll have a different state for each possible number of cards remaining in the deck 11 (only possible before first turn), 10, 9, ..., and 1. The last we'll use as a special state, primarily not to denote when one card is left, but the fact that an event has been drawn. For simplicity, I'll not keep track of how many events have occurred (although we could expand to include that).

So we need a vector representing the probabilities of the initial state, which is known to be 11 cards, so the state vector, $\mathbf{s}$.

\begin{align} \mathbf{s} = \begin{bmatrix} 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{bmatrix} \end{align}

Here each subsequent entry in the vector represents a different state, and the values are the probabilities of being in each state.

We also need the transition matrix. That is, given a state, what are the probabilities of moving to another state. Consider when there are $c$ cards left. There are three or four relevant possibilities, depending on how you count.

1. You could draw a number card, leaving $c-1$ cards, which occurs with probability $(c-2)/c$.
2. You could draw a shuffle card (probability $1/c$, and then draw a number card (probability $9/10$, as we can ignore drawing the shuffle card again), leaving 10 cards with probability $1/c \cdot 9/10$.
3. You could draw an event card, with probability $1/c$, and end up in the special event state (by our reckoning).
4. You could draw a shuffle card (probability $1/c$) and then draw the event card (probability $1/10$), and end up in the special event state with probability $1/c \cdot 1/10$.

We can combine 3 & 4 to find the total probability of getting an event, which is $1/c + 1/c\cdot1/10 = 1/c \cdot 11/10$.

For the first round the probabilities are a little bit special, as we have 11 cards. Thus, the shuffle card doesn't do anything but delay the game. The two possible outcomes are draw a number card (probability $9/10$) and draw an event card (probability 1/10).

Putting this together, we have the transition matrix, $\mathbf{P}$. Each column represents the initial state, and each row represents the next state, in both cases starting with 11 remaining cards, descending to 2, and ending with the special event state.

\begin{align} \mathbf{P}& = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{9}{10} & \frac{9}{10}\cdot\frac{1}{10} & \frac{9}{10}\cdot\frac{1}{9} & \frac{9}{10}\cdot\frac{1}{8} & \frac{9}{10}\cdot\frac{1}{7} & \frac{9}{10}\cdot\frac{1}{6} & \frac{9}{10}\cdot\frac{1}{5} & \frac{9}{10}\cdot\frac{1}{4} & \frac{9}{10}\cdot\frac{1}{3} & \frac{9}{10}\cdot\frac{1}{2} & 0 \\ 0 & \frac{8}{10} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{7}{9} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{6}{8} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{5}{7} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{4}{6} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \frac{3}{5} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{2}{4} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{3} & 0 & 0 \\ \frac{1}{10} & \frac{11}{10}\cdot\frac{1}{10} & \frac{11}{10}\cdot\frac{1}{9} & \frac{11}{10}\cdot\frac{1}{8} & \frac{11}{10}\cdot\frac{1}{7} & \frac{11}{10}\cdot\frac{1}{6} & \frac{11}{10}\cdot\frac{1}{5} & \frac{11}{10}\cdot\frac{1}{4} & \frac{11}{10}\cdot\frac{1}{3} & \frac{11}{10}\cdot\frac{1}{2} & 1 \\ \end{bmatrix} \end{align}

Note a check that we can do is that each column must sum to 1. That is, the probability of transitioning from one state to one of the states is 1. This is because all possible states are incorporated in the matrix.

To find the probability of each state in round $r$, we just compute $P^r \cdot s$. I've done this for 1–100 rounds below. It's quite rare for a game of 50 rounds to have no events. Also note that after about 10 rounds we seem to have reached a stable condition, where the probabilities of being in each of the states isn't changing much (relative to total probability of not having had an event yet).

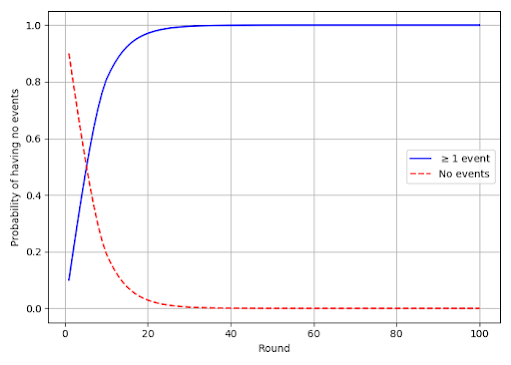Figure 1: Probabilities of having some and no events

Figure 2: Probabilities of having no events, log scale

We can expand this solution to not only look at the probability of whether or not an event has occurred, but instead to look at the probability of an event in any given round. The most straightforward application of the previous method would be to (nearly) multiply the number of states by the number of events possible (i.e. the number of rounds). This keeps track of however many events that we may be interested in, just as we've kept track of the binary state of whether any events have occurred. However, this is very inefficient and quickly leads to very large matrices. Instead, we can take note of the fact that if we look at the current round, the only thing that affects whether we draw an event is whether it is still in the deck, not how many times we've drawn an event previously. Thus, we can merely (roughly) double the number of states, with about half corresponding to the cases where the event card is in still in the deck, and the rest corresponding to the cases where the event card has already been drawn. The first state is again one with 11 cards left, which is equivalent to the case when there is 1 card left. If one card is left, it must be the reshuffle card, which, when drawn at the beginning of the next round, then leaves 11 cards just as at the start of the game. The next 9 states are when 10–2 cards remain in the deck, including the event card. The final 9 states are when 10–2 cards are left in the deck, but the event card is not in the deck.

The probabilities are much as before, except that we now broken up cases 3 & 4 from above, and we consider the transitions between the various number of possible cards left in the deck without the event card. The probability of decreasing by one card in the deck, both without the event card, is the probability of not drawing the reshuffle card, $(c-1)/c$. Also note that when there are two cards left there's a probability of $0.5$ that the reshuffle card remains. This is equivalent to the the initial state of having 11 cards, as previously mentioned, as is why the probability of moving from the two 2-card states to the 11-card state is $1/2$.

From any of these states, we can compute the probability of drawing a card. This actually is equal to the sum of elements of the matrix we just constructed. We need to sum the elements which correspond to moving from a state with the event card in the deck to one without it. This includes the cases when the reshuffle card is drawn. To this we must add the cases when the event card is initially out of the deck, the reshuffle card is drawn, and finally the event card is drawn. That is, the 11th row all counts. We must also consider the $1/2$ probability that we go from 2 cards with event to 11 cards left, as this really represents drawing the event card and leaving only the reshuffle card in the deck. Using this we can construct a matrix, $\mathbf{G}$, with all of these probabilities are the elements, such that when we multiply it by any probabilistic state vector, we get the probability of drawing an event card from that state.

Using these three we can find the probability of drawing an event in any round.

\begin{align} P(\text{event in round } r) = G P^r s \end{align}

The result of this equation is plotted in Fig. 3. We see a perhaps somewhat unexpectedly consistent result that appears to be exactly equal to 0.1. But is it? Does this continue forever? We can certainly easily compute the probability for any practical number of rounds, and any deviation from exactly 0.1 in our computations appears to be due to computer rounding error.

Figure 3: Probabilities of drawing an event in current round

So let's prove it. First, we'll quickly dispense with the simple case when there are 11 (or 1) cards left in the deck. Here we must end by drawing a non-reshuffle card, of which there are ten with only one being an event. Thus the probability of drawing an event given that there are 11 cards left is $1/10$.

\begin{align} P(\text{event} | C = 11) = 0.1 \end{align}

Note a slight change in notation here. After writing the above equation, it became obvious that the number of cards left is really a random variable, and hence the switch to a capital $C$. The rest of the cases rely on some observations about the relationship between having an event card in the deck and not when there are given number of cards, $c$, left in the deck. That is, given $C$, what is the probability that the event card is still in the deck?

\begin{align} P(\text{event in deck} | C = c) = ? \end{align}

Let's consider how we get to having $c$ cards left at the beginning of a round. For this to happen, in the rounds immediately preceding the $11-c$ cards not in the deck must have been drawn. What is the probability of doing that while leaving the event card in the deck? Keep in mind that this is conditioned on not drawing the re-shuffle card in any of these rounds.

\begin{align} P(\text{draw value} | \text{don't shuffle}, C=c) = \frac{c-2}{c-1} \end{align}

We need to multiply this term depending on the number of cards left.

\begin{align} P(\text{event in deck} | C = c) &= \prod_{i=11}^{c-1} \frac{i-2}{i-1} \\ \require{cancel}&= \frac{\cancel{9}}{10} \cdot \frac{\cancel{8}}{\cancel{9}} \cdot \frac{\cancel{7}}{\cancel{8}}\cdots \frac{\cancel{c}}{\cancel{c+1}} \frac{c-1}{\cancel{c}} \\ &= \frac{c-1}{10} \end{align}

The probability of drawing an event depends on whether or not the event card is still in the deck. These probabilities largely follow from our initial analysis.

\begin{align} P(\text{event} | \text{event in deck}, C = c) &= \underbrace{\frac{1}{c}}_{{\text{draw event directly}}} + \underbrace{\frac{1}{c}\cdot\frac{1}{10}}_{{\text{draw reshuffle then event}}} \\ P(\text{event} | \text{event not in deck}, C = c) &= \underbrace{\frac{1}{c}\cdot\frac{1}{10}}_{{\text{draw reshuffle then event}}} \end{align}

When the event is not in the deck, the only way to draw it again is to first draw the reshuffle. Putting these together we can find the following.

\begin{multline} P(\text{event in deck} ) = P(\text{event} | \text{event in deck}) \cdot P(\text{event in deck}) \\+ P(\text{event} | \text{event not in deck}) \cdot \left ( 1 - P(\text{event in deck} ) \right ) \end{multline}

In our case (conditioning on $C=c$), we can find what we're looking for.

\begin{align} P(\text{event in deck} | C = c) &= \left (\frac{1}{c} + \frac{1}{c}\cdot\frac{1}{10} \right ) \cdot \frac{c-1}{10} + \frac{1}{c}\cdot\frac{1}{10} \cdot \left ( 1 - \frac{c-1}{10} \right ) \\ &= \frac{1}{c} \cdot \frac{11}{10} \cdot \frac{c-1}{10} + \frac{1}{c} \cdot \frac{1}{10} \cdot \frac{11-c}{10} \\ \require{cancel}&= \frac{11\cancel{c}}{100\cancel{c}} - \cancel{\frac{11}{100c}} + \cancel{\frac{11}{100c}} - \frac{\cancel{c}}{100\cancel{c}} \\ &=\frac{11}{100} - \frac{1}{100} \\ &= \frac{10}{100} \\ &= \frac{1}{10} \end{align}

Here we see that, indeed, regardless of how many cards there are in the deck, the probability of drawing an event always works out to be exactly 0.1. Here two effects exactly cancel each other out. On the one hand, when there are fewer cards, it's more likely to draw an event card that is still in the deck. On the other hand, with fewer cards it's less likely that there the event card still is in the deck.

There is yet a simpler way to see that the probability of drawing an event every round is 0.1. Consider the symmetry of the situation. Every round ends with a non-reshuffle card being drawn. There is no difference in the 10 non-reshuffle cards that impacts the probability of them being drawn. Therefore, the probability that each is drawn in any round must be 0.1. You may ask whether drawing the event card affects the probability of it being drawn in a subsequent round. It does; that effect shows up in certain conditional probabilities.