Is there a flaw in Savage Worlds?

You might ask:

I've read that there's a flaw in the way the dice work in Savage Worlds. Can you explain that?

Sure... Let me first say that I disagree that there's a flaw; the designers made a valid design tradeoff (though, just as with my Battletech partial cover analysis, I don't have any knowledge of the actual decision-making process). Let's go through the claim and the math behind it.

In Savage Worlds, in general, you're rolling a die and trying to get 4 or higher. (Getting higher multipliers may also be good, but let's keep things simple.) You roll a different size die depending on what skill or ability you're rolling. You may roll 1d4, 1d6, 1d8, 1d10, or 1d12. (You'll also roll a "wild die'' with this, a 1d6, which we'll ignore for now.) If you roll the maximum possible for the die you are rolling, you get to roll again and add the results. That is, if you roll $N$ on 1d$N$, you roll 1d$N$ again, and take $N$ plus the result of the second roll as your total result. You can keep doing this as long as you keep rolling the maximum. So you if you are rolling 1d6, and roll 6, 6, 6, 3, then your total result is 21.

Wow, doesn't this mean that you can roll infinitely high? Yes.

So what's the probability distribution look like? Let's continue to work with 1d6 for the moment. If we roll 1–5, we know the probability is $1/6$. Let's say our total result is $Y$.
\begin{align}
P(Y=y) = \frac{1}{6} \quad y \in \{1,2,\cdots,5\}
\end{align}
Interestingly, the probability of getting a $Y= 6$ is zero. This is because when you roll a 6 you roll another die and add the result. The minimum you get on the second die is 1. The probability of getting 7–11 is,
\begin{align}
P(Y=y) ,\ y \in \{7,8,\cdots,11\} &= P(\text{first roll 6}) \cdot P(\text{then roll }y-6) \\
& = P(Y_1 = 6) \cdot P(Y_2 = y_2) ,\ y_2 = y-6 \\
& = \frac{1}{6} \cdot \frac{1}{6} \\
& = \frac{1}{36} \approx 0.0278.
\end{align}
Here we've introduced $Y_1$ and $Y_2$ to simplify our equations, where $Y_i$ refers to the $i$-th roll of the die to determine the total sum. Most of the time you'll only roll once, unless you get a 6.  Similarly to the $Y=6$ case, $P(Y=12) = 0$. And then
\begin{align}
P(Y=y) &,\ y \in \{13,14,\cdots,17\} \\
& = P(Y_1 = 6) \cdot P(Y_2 = 6) \cdot P(Y_3 = y_3) ,\ y_3 = y-12 \\
& = \frac{1}{6} \cdot \frac{1}{6} \cdot \frac{1}{6} \\
& = \frac{1}{216} \approx 0.00463.
\end{align}
We can see that this pattern will continue, but how do we express it without going on and on? Or, what patterns are we seeing?

Well, we see that the probability of rolling exactly $6k$ is zero. If we have a sum of $6k$ that means we've rolled the die $k$ times and gotten a 6 each time. But if we rolled a 6 last, then we need to roll again and add the result, which is more than 0. Thus it's impossible to get a result of $Y = 6k$, so the probability is zero.

We also see the the probability of getting any particular result if we rolling the die $k$ times is $\left(\frac{1}{6}\right)^k$. For a result of interest, $y$, $k = \left \lfloor \frac{y}{6} \right \rfloor$, which is just $y/6$ rounded down.

So in general,
\begin{align}
P(Y=y) = \begin{cases}
\left(\cfrac{1}{6}\right)^{k+1} & 6k < y < 6(k+1) \quad y,k \in \mathbb{W}\\
\quad 0 & y = 6k \quad y,k \in \mathbb{W}.
\end{cases}
\end{align}
Note, I use $\mathbb{W}$ here to refer to the set of whole numbers: 0, 1, 2, etc. You may find other definitions for whole numbers, and caution against using it because of confusion. But it seems more natural than writing $\mathbb{Z^*}$ as Wolfram MathWorld suggests.

We can generalize for an $N$-sided die by replacing $6$ with $N$ in our equations, since 6 was always just representing the number of sides on the die, or the maximum you could get on a single roll, which are the same for the dice used in Savage Worlds.
\begin{align}
P(Y=y) = \begin{cases}
\left(\cfrac{1}{N}\right)^{k+1} & N\cdot k < y < N\cdot(k+1) \quad y,k \in \mathbb{W}\\
\quad 0 & y = N\cdot k \quad y,k \in \mathbb{W}
\end{cases}
\end{align}
Let's look at the results for a few common die sizes.

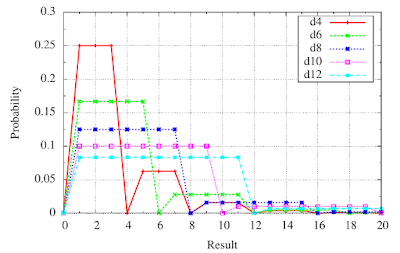Fig. 1: Probability mass functions (PMFs) of exploding dice.

There's not much telling in Fig. 1, which plots PMFs for the different dice used in the game. Where it gets interesting is when we plot the cumulative distribution function (CDF).

Recall that the CDF $F_Y(y) = P(Y \leq y)$. We can compute this as the sum of the probability mass function that we just derive and plotted.
\begin{align}
F_Y(y) = \sum_{k=-\infty}^y f_Y(k),
\end{align}
where $f_Y(y)= P(Y=y)$ is the probability mass function. This function is plotted in Fig. 2. However, we're interested in the probability that we roll a certain value, or higher. This probability, $P(Y \geq y)$ is a sort of complement to the CDF, which we found to be follow the relation,
\begin{align}
P(X \geq x) = 1 - F_X(x+1).
\end{align}

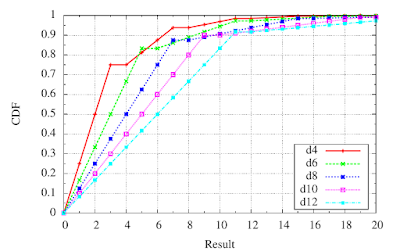Fig. 2: Cumulative distribution functions (CDFs) of exploding dice.

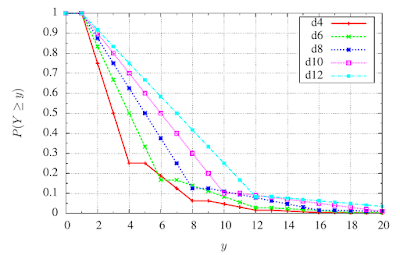Fig. 3: $P(Y \geq y)$

As you can see in Fig. 3, rolling a higher-sided die is not always better. For example, if you compare the plots for a d4 and a d6, you can see that the probability of rolling a 6 or higher on a d6 is actually lower than doing so on a d4. This is similar for other dice when trying to roll $N$ or higher on a d$N$ compared to d$(N-2)$.

This is an unexpected result, and certainly seems undesirable; skills and stats with higher dice are supposed to be better. Let's quantify how undesirable. We'll look at two avenues. First, does this actually affect the game? That is, are we ever trying to roll a 6? Well, a 6 specifically, no. You are trying to roll 4 or higher in general, and in some cases trying to get multiples of 4. So you may be trying to get 8, which is also a point where this happens. A d6 has a higher chance of rolling an 8 or higher than a d8 does.

Second, let's quantify the difference in probability. It looks quite small on the plot, but let's compute it here. The probability of rolling an 8 or higher on a d8 is simple enough, it is $1/8$. What about on an exploding d6? Well, the probability of rolling 6 or higher is $1/6$. Given that we first roll a 6, you then just need to roll a 2 or higher. Thus,
\begin{align}
P(Y_6 \geq 8) &= P(\text{first roll 6})\cdot P(\text{then roll 2 or more}) \\
&= \frac{1}{6}\cdot \frac{5}{6} \\
&= \frac{5}{36} \\
& \approx 0.139.
\end{align}
Comparing that to the probability on a d8: $1/8 = 0.125$. The difference is
\begin{align}
\frac{5}{36} - \frac{1}{8} &= \frac{5}{2 \cdot 2 \cdot 3 \cdot 3} - \frac{1}{2 \cdot 2 \cdot 2} \\
&= \frac{5 \cdot 2}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 2} - \frac{3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} \\
&= \frac{10}{72} - \frac{9}{72} \\
&= \frac{1}{72} \\
& \approx 0.0139.
\end{align}
Above I did a prime factorization of 36 and 8, so that I could find the least common multiple in order to get a common denominator to do the subtraction and get the exact result. Since we're not doing anything further with the result there's not much concern for numerical rounding issues here, so you could also just do the subtraction with a calculator.

So this is saying that an exploding d6 is slightly better than a d8 at rolling 8 or higher. It's better by about 0.0139. But that's not actually the full story. Because in Savage Worlds, player characters and notable NPCs are "Wild Cards''. This means they get the mechanical benefit of always rolling an additional exploding d6 and taking the better of the two results. How does that change the probabilities? Intuitively, I'm going to say that it's going to bring them closer together. That's because for both cases they're going to have the same probability of getting 8 or higher on the wild die. But let's quantify it. The wild die only makes a difference when you don't roll 8 or higher on the first die. Let's say the result of rolling the d6 with a wild die is $W_6$, while the d8 with a wild die is $W_8$. Let's rename to $X$ the result of an exploding die, $X_6$ for d6, $X_8$ for d8.
\begin{align}
P(W \geq w) = P(X \geq w) + P(X < w) \cdot P(X_6 \geq w)
\end{align}
We already computed $P(X \geq w)$ and $P(X < w)$ is simply $1 - P(X \geq w)$, so
\begin{align}
P(W \geq w) = P(X \geq w) + (1 - P(X \geq w)) \cdot P(X_6 \geq w).
\end{align}
Let's compute the one's we're specifically interested in.
\begin{align}
P(W_6 \geq 8) &= P(X_6 \geq 8) + (1 - P(X_6 \geq 8)) \cdot P(X_6 \geq 8) \\
&= \frac{5}{36} + \left(1 - \frac{5}{36}\right) \cdot \frac{5}{36} \\
&= \frac{5}{36} + \frac{31}{36} \cdot \frac{5}{36} \\
&=\frac{5\cdot 36}{36\cdot 36} + \frac{31\cdot 5}{36\cdot 36} \\
&=\frac{5\cdot (36+31)}{36\cdot 36} \\
&=\frac{5\cdot 67}{36\cdot 36} \\
&=\frac{335}{1296} \\
&\approx 0.258
\end{align}
\begin{align}
P(W_8 \geq 8) &= P(X_8 \geq 8) + (1 - P(X_8 \geq 8)) \cdot P(X_6 \geq 8) \\
&= \frac{1}{8} + \left(1 - \frac{1}{8}\right) \cdot \frac{5}{36} \\
&= \frac{1}{8} + \frac{7}{8} \cdot \frac{5}{36} \\
&=\frac{36}{8\cdot 36} + \frac{7\cdot 5}{8\cdot 36} \\
&=\frac{36+35}{8\cdot 36} \\
&=\frac{71}{8\cdot 36} \\
&=\frac{71}{288} \\
&\approx 0.247
\end{align}
The difference is
\begin{align}
P(W_6 \geq 8) - P(W_8 \geq 8) & = \frac{335}{1296} - \frac{71}{288} \\
& = \frac{335}{36\cdot 36} - \frac{71}{8 \cdot 36} \\
& = \frac{335}{36\cdot 36}\cdot \frac{2}{2} - \frac{71}{8 \cdot 36} \cdot \frac{9}{9}\\
& = \frac{335\cdot 2}{72\cdot 36} - \frac{71\cdot 9}{72 \cdot 36} \\
& = \frac{670-639}{72\cdot 36} \\
& = \frac{31}{2592} \\
& \approx 0.0120.
\end{align}
So the difference got smaller, but not much smaller. But recall the absolute difference is still small. What would it take to notice this difference in probability? In other words, let's say you didn't do the analysis, but did pay very close attention to all the rolls you make. How many rolls in a session to have confidence that something was weird about the probability distributions themselves? (Later, we'll discuss whether your dice are even good enough to guarantee probabilities to this accuracy.) I don't want to get into hypothesis testing and statistical analysis here. So let's just ballpark it. Out of 100 rolls where you were trying to get 8 or higher, you'd expect to succeed about 1 more time with the d6 as opposed to the d8. (Yes, expect as in expectation, and the expected value.)

However, since the individual probabilities are about $1/4$, we'd also expect to see some substantial variation in the number of successful rolls out of 100. We can use the binomial distribution. The standard deviation, $\sigma$, for a binomial distribution for 100 rolls and probability of success $p=0.25$ (both of our cases are quite close to this) is
\begin{align}
\sigma &= \sqrt{np(1-p)} \\
&=\sqrt{100 \cdot 0.25 \cdot (1 - 0.25)} \\
&=\sqrt{18.75} \\
&\approx 4.33.
\end{align}
(You can look up the binomial's variance on Wikipedia, which is the square of standard deviation.)

This means that we expect the deviation about the mean to be about 4.33. Now, this isn't a normal distribution, so we can't say that 68% of the time we'd get a result within 4.33 of the mean. However, since the standard deviation is larger than the difference in expectation, it's going to be very unlikely that anyone would conclude that $P(W_6 \geq 8) > P(W_8 \geq 8)$ just by looking at the results, even after observing 100 rolls. You'd need to look at many more rolls.

Also, note that for rolling 4 or higher (or 12 or higher for that matter), which is what you want much of the game, the d8 is still notably better than a d6. Looking at the probabilities in Fig. 3, we can see the probability on a d8 of getting 4 or higher is more than 0.1 higher than on a d6. That's more than 10 percentage points.

On the other hand, if only for beauty's sake, I see the desire for monotonically increasing probabilities with larger die sizes for all target numbers. (Monotonic means that one thing always moves in the same direction (increasing or decreasing, as the case may be) when something else moves in a given direction. In general, if something is occasionally flat we may still say it is monotonic. But something that is strictly monotonic never stops changing, although it may slow down.) There are ways to do this; I have considered two, but they both have costs. They both stem from the observation in Fig. 3 that the probability is flat between $N$ and $N+1$, since there is zero probability of getting a result of $N$. If this were not the case, then the $P(Y\geq y)$ would fall at $N+1$, and maybe we wouldn't have this non-monotonicity.

In the first method, you use differently labeled dice. Instead of numbering an $N$-sided die from 1 to $N$, you could number it from 0 to $N-1$. Now you "Ace'' when you get a roll of $N-1$. Note here though, that since your second roll may be 0, you have a non-zero chance of getting any non-negative final result. At least for now, I'll leave it as an exercise for the reader to prove that this makes larger-sided dice better for all target numbers. What are the costs of this approach? First, literal dollars. Such dice are not common. There are percentile d10 that are marked 00 through 90 which could be read as 0–9. Indeed, you could just tell players to treat a 6 as a 0 on a normal d6. However that's not going to make as streamlined a player experience, and players will have to diligently remember their dice mean something different than what they say. So then players either need to find such dice, or Pinnacle would have to include them with the game.  (Pinnacle Entertainment Group is the publisher of Savage Worlds.) That raises a cost barrier to entry. Second, it's going to be awkward when totaling the result after exploding. You exploded twice on your d4 and then rolled a 2. So you result is $3+3+2=8$. It's much more natural to add the number of faces on the die.

In the second method, you add a roll to confirm that you are going to explode. You could do this in a variety of methods. If going with this approach, I would suggest you just roll the die again. If you roll anything except a 1, you do indeed explode and roll again and add that result. Thus the probability of getting an 8 or higher on such an exploding d6 is $\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}=\frac{25}{216}\approx0.116$, which is less than the probability of rolling 8 or higher on a d8 ($1/8=0.125$). The cost here is in time. You have to make an extra roll every time you might explode a die.

Thus, we can see that there's a tradeoff here. For a game that emphasizes speed of play, a valid—and I daresay correct—design decision was made to make a very slight sacrifice in the probabilities to win out on accessibility and resolution time.


As a fun aside, you can actually use probability here to prove the existence of convergence and sum of the series here. For example, let's take the case when $N=2$. Here we're basically flipping a coin labeled 1 and 2. We know $P(Y \leq 1) = \frac{1}{2}$, and thus $P(Y > 1) = 1 - P(Y \leq 1) = 1 - \frac{1}{2} = \frac{1}{2}$. Since $P(Y > 1)$ can be written as,
\begin{align}
P(Y>1) &= \sum_{y=2}^\infty P(Y=y) \\
&= \sum_{y=2}^\infty \begin{cases}
\left(\cfrac{1}{2}\right)^{{\left\lfloor\cfrac{y}{2}\right\rfloor}+1} & y \text{ odd}\\
\quad 0 & y \text{ even}
\end{cases}.

\end{align}
Note here that $\left\lfloor x \right\rfloor$ refers to the floor of $x$, which is $x$ rounded down to the nearest lower integer.

We can rearrange to get rid of the cases statement easily enough. Instead of summing all the odd $y$ starting at $y=2$ above (well, $y=3$, since 2 is even), we can write them as $y = 2\cdot k+1$, and sum over all integer $k$ starting at 1.
\begin{align}
P(Y>1) &= \sum_{k=1}^\infty \left(\cfrac{1}{2}\right)^{\left\lfloor (2\cdot k + 1)/2 \right\rfloor+1} \\
&= \sum_{k=1}^\infty \left(\cfrac{1}{2}\right)^{\left\lfloor k + 1/2 \right\rfloor+1} \\
&= \sum_{k=1}^\infty \left(\cfrac{1}{2}\right)^{k + 1} \\
&= \sum_{k=2}^\infty \left(\cfrac{1}{2}\right)^{k} \\
\frac{1}{2} &= \sum_{k=2}^\infty \left(\cfrac{1}{2}\right)^{k} \\
\end{align}
Our last equality is indeed the result we get from a conventional analysis of the series. The normal derivation goes something like this. Say we're looking for the sum $s$ of the series,
\begin{align}
s = \frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} \cdots .
\end{align}
We can divide both sides of the equation by 2, and then add $\frac{1}{2^2}$, getting
\begin{align}
\frac{1}{2^2} + \frac{s}{2} &= \frac{1}{2^2} + \frac{1}{2} \cdot \left(\frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} \cdots \right) \\
& = \frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} + \frac{1}{2^5}\cdots .
\end{align}
However, distributing the multiplication on the right-hand side as I did above, gives us the same series, which is equal to the sum $s$ we're looking for. Thus we can do some algebra below to find $s$.
\begin{align}
\frac{1}{2^2} + \frac{s}{2} &= s\\
\frac{1}{4} &= s - \frac{s}{2} = \frac{1}{2} \cdot s \\
\frac{1}{4} \cdot \frac{2}{1} &= s \\
\frac{1}{2} &= s.
\end{align}